“Con mucho acento”. Creo que, aunque vio la luz hace pocos días, a estas alturas todos hemos visto ya el anuncio de CruzCampo que “resucita” a Lola Flores gracias a la Inteligencia Artificial (IA). Ha copado minutos en informativos y tertulias de todo tipo. Gracias a él, mucha gente ha descubierto los “deepfakes” y con ello, alguna de las cosas espectaculares que la IA puede hacer. En este caso han sido las Redes Neuronales, y en concreto, las llamadas GAN (Generative Adversarial Networks), que pueden generar contenidos desde cero.
Ellas están detrás de apps que seguro muchos hemos usado, como FaceApp, que nos ha permitido jugar a vernos a nosotros y a nuestros amigos y familiares con 20 o 30 años más. O incluso detrás de un cuadro, como el Retrato de Edmond Belamy, vendido por la prestigiosa galería Christie’s por $432.500. Una “obra de arte” creada por IA. De hecho, la firma del autor que aparece en el cuadro es una fórmula:

Y es una fórmula porque, detrás de todo esto no hay otra cosa que matemáticas. Estas son la base de todo esto de lo que tanto se está hablando estos días: Redes Neuronales, deep learning, deepfakes… Sin matemáticas nada de esto es posible. No es mi objetivo hoy en este artículo ni aburrir con complejas matemáticas ni hacer un tratado exhaustivo de IA, solo dar dos pinceladas de la importancia de las matemáticas detrás de todo esto, y de que aquello que veíamos en el colegio, y que hoy estudian nuestros hijos en 4º ESO sirve para algo, o mejor dicho, para mucho. Como no pretende ser un tratado profundo de IA, voy a simplificar algunos conceptos.
Empecemos por la base, las Redes Neuronales. Una Red Neuronal la podemos ver como una serie de capas de nodos simples (tan simples como que principalmente suman y multiplican – matemáticas básicas, ¿no? – bueno, y alguna operación más), conectadas entre si. De ellas, hay una capa de entrada que recibe unos datos, y otra última de salida, que los clasifica. Así, la entrada puede ser por ejemplo fonemas cuando hablamos a una de esas máquinas que atienden llamadas, y la salida, la interpretación de qué palabra he dicho. La magia de las Redes Neuronales es que aprenden solas… o casi solas: les damos una serie de casos con sus soluciones, y la propia red va ajustando esas “sumas y restas” que hacen sus nodos para que el resultado final que da esa capa de nodos de salida se vaya pareciendo al resultado esperado. La diferencia entre los resultados esperados y los que obtiene la Red Neuronal se llama Error o Coste, y obviamente, el objetivo en el aprendizaje de la Red es minimizar esa función. ¿Cómo se minimiza? Pues con algo que todos aprendimos, más o menos, en el colegio: las derivadas. Sé que tú te acuerdas, pero por si algún lector no, recuerdo que una derivada te daba la pendiente de una gráfica (lo recordamos, ¿verdad?). Podemos ver la función error (o coste) de la Red Neuronal como un monte, con sus colinas, y donde yo quiero llegar al punto más bajo (mínimo error). Si en el monte voy mirando las pendientes de las cuestas, aquí lo que vamos viendo son las derivadas (pendientes) para llegar al punto más bajo. Sencillo, ¿no? … y mira, de paso ya sabemos un uso práctico de aquellas derivadas que nos enseñaban en clase.
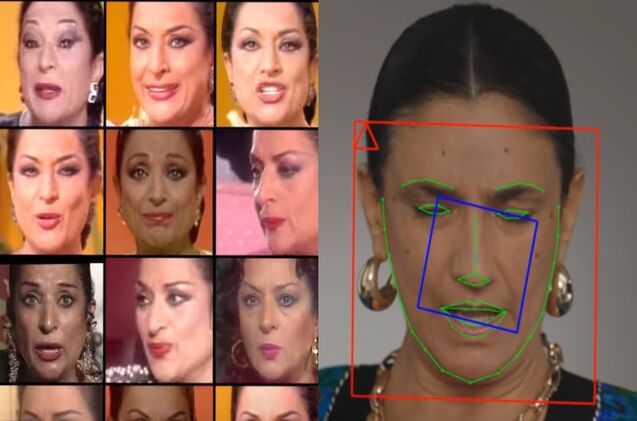
Con esto ya tenemos la base de las Redes Neuronales. Vamos a ver ahora, también simplificando todo lo posible para no perder al lector, cómo se genera contenido como el del video de Lola Flores. Aquí surge un concepto que creó un investigador llamado Ian Goodfellow: las GAN (“G”enerative “A”dversarial “N”etworks) y que ha revolucionado el mundo de la IA. Su modelo se basa en dos Redes Neuronales (de ahí la “N”) compitiendo entre si (de ahí la “A”) con el objetivo de generar contenido (de ahí la “G”). Una de esas redes se dedica a generar contenido no real (esa red se llama “Generador”) e intentar engañar a una red (que se llama “Discriminador”) cuya función es distinguir qué contenido es real y cuál es falso, es decir, procedente del Generador. Por ejemplo, la red Generador produce fotogramas de Lola Flores y la red Discriminador trabaja en distinguir si es una imagen real, sacada de alguna foto de la artista, o si en cambio ha sido generada.
Las dos redes van aprendiendo: el Generador a hacer fotogramas de Lola cada vez mejores, cada vez más cercanas a confundir al Discriminador, y este a su vez va mejorando su criterio para distinguir. Con ello, según mejora el Discriminador, más se tiene que esforzar (aprender a hacer imágenes falsas realistas) el generador.
Detrás de este proceso de mejora de las dos redes, hay, como no puede ser de otra manera, más matemáticas. Como toda Red Neuronal que se precie, necesita su función de error. Si asumimos que etiquetamos con un “0” las imágenes de Lola generada, y con “1” las Lolas reales, la función error debería de darnos un valor muy bajo, idealmente 0, cuando el Discriminador clasifique correctamente, y lo más alto posible (infinito), cuando falle. En matemáticas, la función que hace lo más parecido a esto es el logaritmo. De hecho, para las Lolas reales, la función de error es E=-log(x) (para el que no la recuerde, esta función en “0” tiende a infinito y en el “1”, es cero). Para las Lolas del anuncio de Cruzcampo, pues E=-(1-log(x)), que es una gráfica justo al revés. Y ahí están, Generador y Discriminador luchado por maximizar o minimizar el error. Esto ya se va pareciendo a algo que hemos visto al principio, ¿recurdas?. Efectivamente, es la firma del autor del cuadro vendido en Christie’s (bueno, hay matiz de un signo, pero no vamos a liarnos más en este punto). Y es que esta firma representa la magia de las GAN, y con ellos de los deepfakes como el del video de Lola Flores. Es decir, detrás de todo esto, hay pura matemática: sumas, restas, derivadas, unos logaritmos, alguna matriz…
Por eso no podemos descuidar las matemáticas. Si queremos como país jugar en alguna de las ligas importantes donde es está diseñando el futuro, este futuro pasa por tecnologías como la Inteligencia Artificial. Está llamada a hacer anuncios como hemos visto, pero también otras cosas más importantes como ayudar a desarrollar vacunas y medicinas, a hacer diagnósticos o incluso será clave en el mundo del automóvil. Es fundamental con ello apostar en la educación de nuestros jóvenes por la ciencia en general, y la base de todo este futuro, que son las matemáticas y la programación. No pueden ser una asignatura más, hay que darle la importancia real que tienen, y formar a nuestros profes para que la sepan transmitir. Necesitamos en las nuevas generaciones el bilingüismo tecnológico. Ese tiene que ser nuestro otro acento.